ちょっと脱線になりますが、今回は景気循環の理論的な研究について少し整理したいと思います。景気循環の研究は歴史が古く、1860年代にはウィリアム・スタンレー・ジェボンズやクレメント・ジュグラーなどが研究を行い、1920年代にも、ウェズリー・ミッチェルが全米経済研究所を設立し、統計的な経済変動モデル（経済理論の代わりにサイクルとトレンドに基づくモデル）に基づいた規則的な経済パターンの分析が積極的に行われるなどといった取組がありました。

現代経済学の景気循環理論を整理する際には、ケインズの「雇用，利子および貨幣の一般理論」(1936年）の影臀を受けて、サミュエルソン＝ヒックスによって提示された加速度乗数モデル（Samuelson(1939)、Hicks(1950)）を出発点とすることがよくあるようです。このモデルは、マクロ経済学における国民所得の決定モデルを景気循環に応用したもので、投資についての内生的な決定が波及することによる変動を説明したものです。理論は３本の方程式体系から構成されており、それぞれ

Y_t=C_t+I_t  (1)

C_t=C+cY_t-1  (2)

I_t=I+v(Y_t-1-Y_t-2)  (3)

となります。(1)式は国民所得の決定式、(2)式は消費関数、(3)式は加速度原理の投資関数となります。(2)、(3)式を(1)式に代入すると、以下の2階の差分方程式が得られます。

Y_t=(c+v)Y_t-1-vY_t-2+(C+I)  (4)

この不動点は、Y*=(C+I)/(1-c)、また特性方程式の根（特性根）は、

λ₁,λ₂=((c+v)±((c+v)²-4v)^1/2)/2

となります。システム全体の動学的挙動は、この特性根によって規定されますが、判別式(c+v)²-4vが正となる場合には特性根は実根、負の場合には複素根となることから、それぞれの特徴をみていこうと思います。

特性根が実根の場合には、特性方程式の解と係数の関係から、2実根は共に正であり、また、λ₁,λ₂∈(0 , 1)もしくはλ₁,λ₂∈(1 , ∞)となります。前者の場合には解の軌道は時間とともに不動点に単調に収束し、後者の場合には単調に発散することになります。

特性根が複素根の場合、2根は共役複素数の形で現れ、α+iβ、α－iβと書けます。これらの特性根の絶対値をρ=(α²+β²)^1/2とすると、tanθ=β/α、α=ρcosθ、β=ρsinθとなるので、λ₁=ρ(cosθ＋isinθ)、λ₂=ρ(cosθ－isinθ)と表すことができます。従って、同時部分の一般解を求めると、

a₁λ₁^t+ a₂λ₂^t=2kρ^tcos(tθ＋ε)

となります。因みに今、α＝(c+v)/2、β=((c+v)²-4v)^1/2)/2となるので、ここからρ＝v^1/2となり、v<1→ρ<1の時に解は振動しながら不動点に収束し、v>1→ρ>1の時には、振動しながら発散することになります。

この複素根の2解では、所得水準が均衡水準から乖離して循環的に変動することが示され、投資の変動により景気循環が発生するメカニズムを示すことに成功しています。さらにHicks(1950)はこの複素根に関して、労働や資源の賦存量が制約となって生じるYの天井や、最低限の置換投資や最低限の消費の存在により生じる床の概念を導入して、より詳細な循環現象の解明を行っています。

このように、サミュエルソン＝ヒックスの加速度乗数モデルは、誘発投資のメカニズムを明示的に考慮して、乗数効果と投資の誘発効果の相互作用により、景気の循環的変動を説明することに成功しましたが、これを引き継いで、さらに複雑な景気変動のメカニズムの説明を試みたのが、カルドアやグッドウインになります。これらの理論は比較的類似しているのですが、このうちKaldor(1940)を簡単にみてみたいと思います。

カルドアの研究では、投資関数を非線形にとっています。この投資関数は、利潤原理と呼ばれ、投資が所得水準と資本ストックの水準に依存して決まるとしています。経済の体系に複雑な非線形の投資関数を導入することによって、体系の中に内生的なリミットサイクル（極限閉軌道）が発生する、つまり減衰しない景気循環が生じる可能性があることを示しています。

モデルは、標準的な乗数モデルに利潤原理に基づく投資関数を結合させた1部門の経済モデルで、所得Yと資本ストックKを決定します。投資関数は、①所得が均衡水準を超えて大きくなると、完全雇用に伴う労働供給のボトルネックや、建設費、資金調達コストなどの高騰、ブームの先行きに関する予想が弱気に転じることなどが原因となって、企業の投資意欲が減退し、そのため投資性向が低下する、②所得が異常に低い不況期においては、生産設備の過剰が顕在化し、従って所得が増加しても設備投資はそれほど誘発されない、③生産が十分に大きくなり、過剰投資が解消される中間領域（均衡値の近傍）では、誘発投資のメカニズムが十分に作用し投資性向が高まる、というメカニズムに基づいて構築されており、そのため、投資は資本ストックの減少関数（I_K<0）であり、一方で所得に対しては増加関数であるが、所得水準の近傍から乖離すると限界投資性向が低下する（I_Y>0かつ、Y<Y*ならはI_YY>0でY>Y*ならばI_YY<0）としています。

貯蓄関数については、所得に関して線形の増加関数であるほか、資本ストックが増加すると貯蓄も増加するとしており、0<S_Y<1、S_K>0となります。所得については、財市場における超過需要であるI-Sに依存した、調整係数αの1次関数により調整されると仮定しています。こうした下で、この経済体系の長期的動向は以下の連立微分方程式により示されます

dY/dt=α[I(Y,K)-S(Y,K)]

dK/dt=I(Y,K)-δK

今簡単のため、これらの方程式の不動点（dY/dt=dK/dt=0を満たす解）は一意の解（Y*,K*）を持つと仮定します。この不動点の近傍における動学的安定性を検討するため、連立微分方程式体系を不動点の周辺でテイラー展開した時の線形項を求めると、

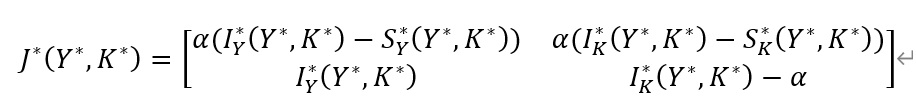
となります。また、特性方程式は

λ²-tr J*λ+det J*=0

となり、この2つの特性根は

λ₁,λ₂=(tr J*±((tr J*)²)-4det J*)/2

となります。また、特性方程式の解と係数の関係から、λ₁+λ₂=tr J*、λ₁×λ₂= det J*が得られます。これを踏まえて、実根と複素根のそれぞれについて、システムの動学的な特性をみてみます。

まず、実根のケースについてみてみます。det J*=λ₁×λ₂>0ならば、2つの固有値は同符号になります。加えて、tr J*=λ₁+λ₂<0ならば、固有値はともに負であり、解軌道は不動点に単調に収束します。この場合、不動点は安定結束点と呼ばれます。

また、tr J*=λ₁+λ₂>0、det J*=λ₁×λ₂>0ならば、固有値はともに正であり、解軌道は正または負の無限大に発散することになり、この場合、システムは不安定結節点を持つといわれます。さらに先ほどの特性根の判別式が正で、従って2実根を持つが、det J*=λ₁×λ₂<0となる場合には、固有値は実数で逆符号の対で現れます。この場合不動点は鞍点安定といわれます。

次に、複素根のケースについてみてみます。この場合特性根の判別式は負で、固有値は共役複素数となり、（α+iβ,α-iβ）のように書くことができます。またこのとき、

α＝tr J*/2、β=(4 detJ*-(tr J*)²)^1/2/2

となります。この場合、固有値の実部が負ならば減衰振動が生じ、最終的に有限値に接近します。これは安定渦状点と呼ばれます。また、固有値の実部が正ならば、振動の振幅は時間の経過につれて大きくなり、不安定渦状点と呼ばれます。幾つかの結果を図にしてみると、以下の様になります。

これをみると、カルドアのモデルの場合、不動点（グラフの真ん中の点）を中心として、ある時は単調に収束し、ある時は発散し、ある時は周回しながら収束・発散していることがわかります。ということは、この不動点付近では発散し、一方でもう少し外側の場所では、その内側でしか運動しないような動きが同時に表現できる根が存在すれば、その根は永続的な景気循環を表していることになります。こうした根が生じる条件については、ポアンカレ＝ベンディクソンの定理で、不動点が一意に決まり、なおかつ不動点が不安定である場合に起こりうることが示されています。また、このサイクルが、先ほど述べたリミットサイクル（極限閉軌道）になります。

このように、カルドアのモデルでは内生的なリミットサイクルも表現できる可能性が示されたわけですが、その後研究は大きく2つの流れに分岐していくことになります。第1のアプローチがスルツキ―＝フリッシュによる不規則衝撃（random shock）の理論というもので、この理論は出発点として安定的な均衡を持つ経済を考え、そこに衝撃が加わると均衡から乖離するわけですが、単発の衝撃ではいずれ減衰していくものの、そこに相次いで衝撃が加わることで景気循環が生じることになります。

また、この第1のアプローチは、不規則衝撃の原因を何に求めるかによってさらに2つの流れがありました。1つがルーカスのマネタリーショック説で、もう1つがリアルショック説です。このうち後者はReal Business Cycle理論として知られています。一方で前者は、不規則衝撃として中央銀行による予期せざる金融政策ショックを考えています。その上で、例えば中央銀行が不意に貨幣を増加させると、その結果として一般物価水準と賃金が上昇しますが、企業はその絶対価格の上昇を相対価格の上昇と誤って判断して生産と雇用を増やすという、事実誤認によって景気循環が生じると説明してました。

もう1つのアプローチは比較的今回紹介した研究に近いといえ、経済に対する予期せざる外生的ショックが存在しなくても内生的に景気循環が発生すると主張するもので、内生的景気循環理論と呼ばれています。これも2つに区分され、１つが最適成長モデルによるもので、もう1つが貨幣経済モデルによるものになります。どちらも、外生的ショックを想定しておらず、また経済のカオス的振る舞いに焦点をあてていることで共通していますが、一方で、前者の変動はパレート最適であるが、後者の変動はそうではないという違いもあります。

こうした点については、次回以降順にみていこうと思います。

Hicks,J.R.(1950).Contributions to the Theory of the Trade Cycle,Oxford University Press.

Kaldor,N.(1940).“A Model of the Trade Cycle,” Economic Journal,50,78-90.

Samuelson,P.A.(1939).“Interactions between the Multiplier Analysis and Principles of Acceleration.”Review of Economic Studies,21,75-78.