今回は経済格差の程度を数値化する指標についてみていこうと思います。こうした指数は決して新しいものではなく、1980年代までに概ね提示されています。最初に出てくるものとして、データのばらつきの程度を表す尺度である分散が考えられます。分散の式は、データをy、データの平均値をμ、データ数をnとして、

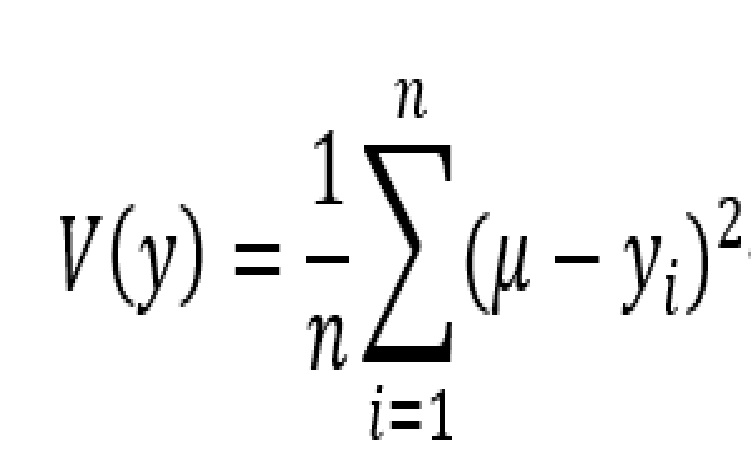
となります。つまり個々のデータの平均値からの乖離を2乗し、その平均をとったものになります。この分散の場合、いくつか問題が指摘されています。例えば、現在は賃金上昇傾向ですが、仮に国全体で同じ割合だけ（a倍とします）賃金が上昇した場合、

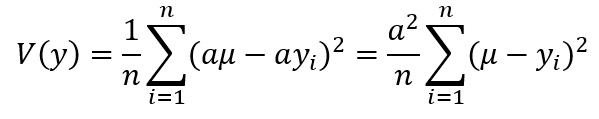
となるので、分散はa²倍だけ大きくなります。また、分散の値はあくまで平均所得からの乖離を数値化しているため、例えば平均所得が低い世界と平均所得が高い世界とでは、分散が同じ値でも所得格差という意味では前者の方が深刻と考えられますが、そこは数値に現れていません。

このうち、最初の問題については、解決策も存在して、個々のデータと平均値について、それぞれ対数値をとって、それを用いて同様に分散をとるというもので、式としては

となります。この場合、先ほどのように国全体の賃金がa倍に増加したとしても、

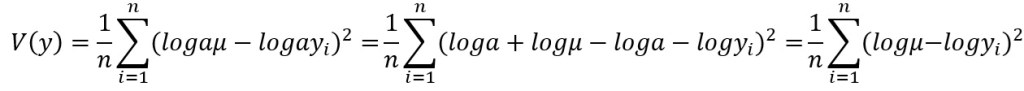
となり、分散の値は変わりません。これは“対数分散”といわれています。

因みに、所得のデータについては、横軸に所得金額、縦軸に頻度をとるようなグラフを書いた場合に、左右対称な分布（例えば正規分布がそう）というよりは、右側に裾が長い（だらだらと続くような）分布になることが知られていて、これは対数正規分布に従うことが知られていますが、データの対数をとることで、変換後のデータは正規分布に近づくことになります。

（注１）対数正規分布というのは、例えばサイコロ投げのような、毎回独立した事象として（加算的に）物事が積み重なっていく正規分布の世界に対して、例えば一国の所得の分布で考えると、若く働き始めたばかりの人もいれば、もう何年も働いている人もいるし、投資にしても、やっていない人、始めたばかりの人、何年も続けている人と色々いるわけで、見ている所得は一時点かもしれませんが、その裏にはそれまでの積み重ねが影響していて、加算的な過程というよりは乗算的な過程になっている世界の分布といえます。因みに、所得分布はほぼ全て対数正規分布に従うのですが、実は上位1％の周辺では、パレート分布（べき分布の一種）という、より裾の長い分布へのあてはまりがよいことも知られています（例えば青木(1979)）。

（注２）所得分布についてはこういう風にも考えられます。例えばIQや身長など、人間の能力・特性には、正規分布に従うものが度々見られます。“やる気”なんかも、世間では２：６：２（よく働く社員２、普通の社員６、働かない社員２）の法則とか言っていますが、正規分布の－1標準偏差～＋1標準偏差間の面積が約６８％で、その外側がそれぞれ約１６％ずつだと考えると、それなりに正規分布といえるかもしれません。他には年齢にしても、正規分布かどうかはわからないですが、所得を多く稼ぐ現役世代で考えれば、それほど分布の裾は長くないでしょう。ただ、所得について考える場合には、これらの要素が組み合わさって影響してしまいますし、他にも、会社を興したらあたったとか、投資で大成功しただとか、そういった要素も（確率は低そうですが…）作用したりすることで、分布の裾が長くなり、対数正規分布や、上位１％なんかはパレート分布に従うようなことが生じます。

この他にも、個々のデータとデータの平均値との差の絶対値も指標として用いられており、平均絶対偏差といわれています。式としては、

となりますが、これは、全員が平均所得を得ている場合、つまり完全に平等な所得分布になる場合には0となります。

ただ、この指標については、平均所得を境として、それよりも所得が高い個人間の所得の移転や、逆に所得が低い個人間での所得の移転は、反映されない（値が変わらない）という特徴もあり、これは不平等の尺度という観点では、問題があると考えられます。

ここまでは平均値からの乖離をみてきましたが、次に紹介するジニ係数は、ばらつきを測る際に平均値を利用せず、全ての個々のデータの組を作って、その差の絶対値を用いて指標を作成するものです。数式としては、

となります。右辺の分子は全ての個々のデータ間の差を全てのデータの組み合わせについてとり、その絶対値の平均値になっています。これと平均値とで比をとったものは相対平均差と呼ばれています。

ジニ係数の特徴は大きく2つあり、1つはローレンツ曲線を用いて直感的な理解が可能なことがあげられます。また2つ目は、個々のデータの値につけられた順位によって、社会厚生を判断する点になります。

2点目については、所得分布を例に考えると、個人を所得の少ない順に番号付けした時に、第i番目の個人の所得のシェアをs_i=y_i/nμとすると、ジニ係数の式は

と書くことができます（導出はSen(1997)）。このため、ジニ係数が各個人の相対的な所得の順位に従って、所得分配を判断していることがわかります。

もう1つ、有名な指標にタイル（Theil）指数というものがあります。この指数はTheil(1967)で開発されたもので、情報理論におけるエントロピーの概念から導出しています。エントロピーは平均的な情報の価値を測る概念で、ある事象x_iが生じる確率をp_iとしたときに、事象x_iの価値をh(p_i)とすると、この関数は確率が高くなるほど減少すると考えられます。情報理論の世界ではこれを満たす関数としてh(p_i)=－logp_iを用いていて、例えばn個の事象が生じる時の平均的な情報の価値を

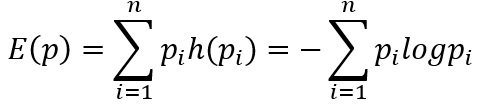
とあらわします。タイル指数は、まず、p_iをs_i=y_i/nμで置き換えて、更に、E(p)は各事象の発生確率が均等な時に最大（logn）となる関数ですが、むしろここでは（他の指数にあわせて）個々人の所得シェアのばらつきが大きくなると値が大きくなるようにしたいので、

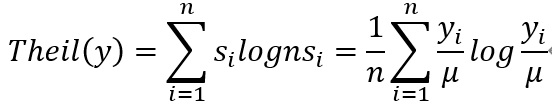
としています。タイル指数の特徴は、指数を人口属性などのサブグループに分解することができることで、数式としては、

となります。

さらにもう1つ、アトキンソン（Atkinson）指数というものもあって、これは加法的な社会厚生関数Σu(y_i)を前提として構築しています。u(y_i)は凹関数としていて、この場合、相対的に所得の高い人から所得の低い人に所得の移転が生じると、社会厚生は必ず増加します。ここで、ある社会厚生の下での、平等に分配された所得は平等分配等価所得（Equally Distributed Equivalent Income）といいますが、それをy_EDE=y|nu(y)(=Σu(y_i))とした時に、アトキンソン指数は、

と書けます。実際の分析では、“ある社会厚生”というのは、現実の社会厚生ということになるわけですが、そのように考えると、アトキンソン指数は、全員に平均所得μが分配されるときの社会厚生を最高とする場合に、現実の分配の下で生じる厚生損失の割合をあらわしていることになります。

このほか、よりシンプルな指標として、異なる所得階層間の比率をとるというものもあります。こうしたもののうち最も有名なのは、所得階層の下位20％（0～20％）と上位20％（80～100％）の所得シェアを比較するS80/S20比率と呼ばれる指標ですが、他にも上位10％（90～100％）や上位1％（99～100％）と比較する指標など、様々なものがあります。

そうした中で、近年急速に使われるようになっている指標に、パルマ（Palma）指数があります。これは所得階層の下位40％（0～40％）と上位10％（90～100％）の比をとるものです。

なぜこの指数が使われるようになったのかというと、こうした指数の欠点として全てのデータを使っておらず、一部の階層の変化のみを追っているということが指摘されているのですが、Palma(2006,2011)が多くの国について、GNIの約半分は、その国の中間層（所得階層の50～90％）の家計が持っていて、それが非常に安定している一方で、高所得層の割合と低所得層の割合については、国によって大きく異なることを指摘し、それから注目されるようになりました。

パルマ指数はCobham and Summer(2013)で提示されたのですが、ここでは、パルマ指数とジニ係数の相関が高いことをデータから示し、十分な説明力を持っているとしています。

パルマ指数は一部の対象しか計測しないかわりに、動きの説明がわかりやすいという利点があることもあり、近年ではSDGs（持続的な開発目標：Sustainable Development Goals）のGoal 10「人や国の不平等をなくそう」のなかでも目標として使われています（Target 10.1”By 2030, progressively achieve and sustain income growth of the bottom 40 per cent of the population at a rate higher than the national average”）。

以上、いくつか指標をまとめてきましたが、次は推計手法を整理したいと思います。

参考文献

Cobham, Alex, and Andrew Summer(2013).”Is it all about the Tails? The Palma Measure of Income Inequality,” Working Papers 343, Center for Global Development, Washington,DC.

Palma, Jose Gabriel(2006).”Globalizing Inequality: ‘Centrifugal’ and ‘Centripetal’ Forces at Work,” Working Papers 35, United Nations, Department of Economics and Social Affairs.

Palma, Jose Gabriel(2011).”Homogeneous Middles vs. Heterogeneous Tails, and the End of the ‘Inverted-U’: It’s All About the Share of the Rich,” Development and Change,42(1),87-153.

Sen, Amartia K.(1997)On Economic Inequality., Expanded Edition with a Substantial Annexe by James E. Foster and Amartya K. Sen, Oxford: Clarendon Press（鈴村興太郎・須賀晃一訳『不平等の経済学－ジェームズ・フォスター、アマルティア・センによる補論「四半世紀後の『不平等の経済学』」を含む拡大版』、東洋経済新報社、2000年）

Theil, H.(1967) Economics and Information Theory, North-Holland, Amsterdam.

青木昌彦(1979)、『分配理論』第二版経済学全集13、筑摩書房