ここからはまず、財政政策による景気刺激策の効果を分析した研究についてみていきたいと思います。財政政策の研究は、いわゆる政府支出の研究と税制の研究があり、さらに政府支出の中でも、政府が実際に消費を行う政府消費や、所得移転といった政策があります。今回はこの中でも、特に政府消費の研究をみていければと思います。

因みに、政府消費というのは、政府が提供する公共サービスのために消費する支出を指していて、具体的には教育、医療、防衛、インフラ整備などの分野での支出が該当します。例えば、比較的大きなウエイトを占めている支出として、健康保険組合などの公的医療保険制度が本人負担分以外の医療費を保険者として医療機関に支払う部分があります（図表１の社会保障基金の現物による社会保障給付）。

　　　　　 図表１.一般政府の最終消費とその内訳（2023年度）

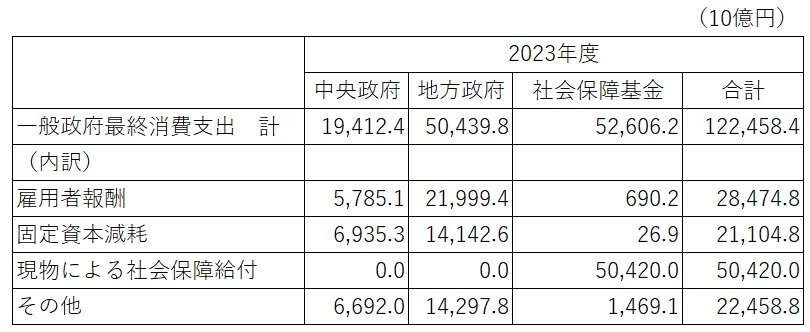
（出所）内閣府「2023年度（令和５年度）国民経済計算年次推計」より筆者作成

ここでは２期間のニューケインジアンモデルを用いて、標準的なモデルから、どのような結果が得られるかみていきたいと思います。

政府部門については、こう考えます。政府は0期、1期にそれぞれG₀、G₁の政府消費を行いますが、この支出の原資は、0期目は国債を発行して賄い、1期目については、国債の償還とG₁分を家計からT₁の一括税を徴収して賄います。そのため、政府の予算制約式はP₀G₀=B₀、P₁G₁+(1+i)B₀=T₁となります。また、家計は政府消費から効用を得ることはないとします。

その上で、モデルは家計部門、製品を生産する生産企業部門、生産された製品を買い取って家計に販売する小売企業部門があると考えます。

ただ、今回のモデルは価格の硬直性があると考えているため、0期については、完全に最適な価格とはならず、一定程度（１－λ）だけ反映されるとしています（一方で、1期目は最終期なので、価格は最適なものが反映されるとしています）。

という関係が得られます。λ≧０としているので、L₀が増加するとP₀も増加しますが、これは製造企業の労働需要が増加すると、最終的に小売価格が増加するという式ですが、これはマクロでみた時に、企業サイドの限界費用の増加と価格の増加の関係式となっているため、フィリップス曲線であることがわかります。

もう１つ、（２）について、

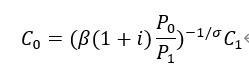
と変形して、ここに（５）を代入することで、

という式を得ます。この式は総需要曲線で、一方で先ほどのフィリップス曲線は総供給曲線なので、この2本の式からAS-ADダイアグラムを書くことができます（図表2）。これを用いながら、みていこうと思います。

　　　　　　　図表2.AS-ADダイアグラム（0＜λ＜1のケース）

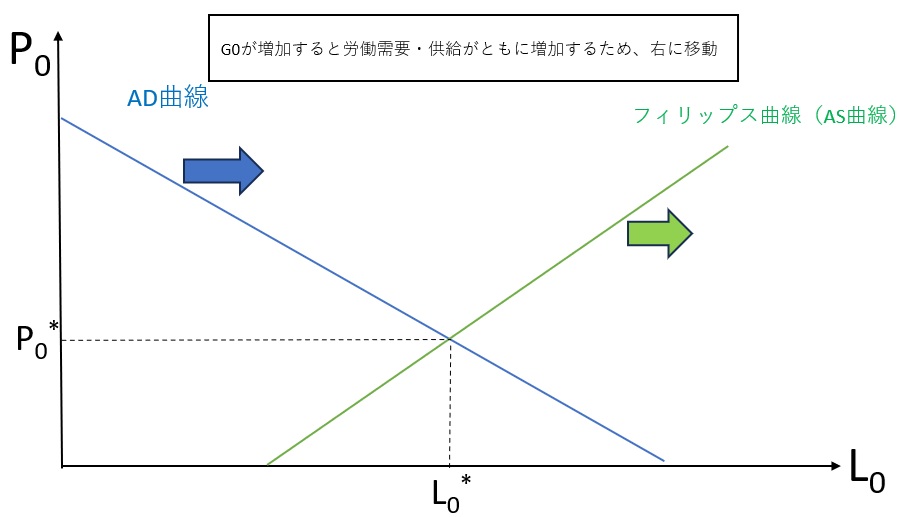
（出所）筆者作成：P₀^*、L₀^*をスタート地点の値として進めます。

とりあえず、大まかな方向性をみてみましょう。まず、総需要曲線（AD曲線）ですが、G₀が上昇すると、同じP₀に対して、L₀は増加することになります。一方でフィリップス曲線（AS曲線）ですが、こちらについても、G₀が上昇するときに、同じP₀に対して、L₀が増加します。

一体、これは何が起こっているんだということですが、G₀が上昇する場合、企業にとっては世の中の総需要が増加することになるため、労働需要が生まれます。一方で家計にとっても、G₀が上昇する時、その財源はB₀なわけですが、要は第1期（将来）の増税で賄うことになるということで、0期の家計にとっては一見関係がないように思えるのですが、家計は消費を生涯で平準化する特性があるので、将来（第1期）の増税というのも、C₀の低下要因となってしまいます（リカードの等価定理）。こうした事情から、家計の側としても、労働供給l₀を増加させることになるわけです。市場清算条件から、l₀=L₀であるため、それがどの辺でバランスするんだということになるのですが、次はλの値を変えてみていこうと思います。

最初にλ＝1の時のケースをみていこうと思います。この場合、フィリップス曲線の形が変わるのですが、今の場合、P₀=P₀^*となります。これはつまり、完全に価格が硬直的な経済のケースといえ、グラフにした場合には、横一直線の直線となって、総需要曲線とあわせると、図表3のように書くことができます。

では、G₀が増加するとどうなるのかというと、価格は変わらず、同じ価格水準に対して、L₀が増加するところにAD曲線とAS曲線の交点がくる、ということになります。

　　　　　　　　 図表3. AS-ADダイアグラム（λ＝1のケース）

（出所）筆者作成

また、もう少し話を進めて、産出Y₀に対してどんな影響があるのか（つまり、財政乗数がどうなるのか）を考えてみましょう。今の場合、Y₀=C₀+G₀であるので、G₀が増加する時のY₀の増加というのは、

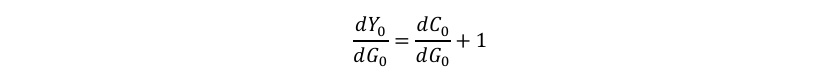
と書くことができます。この時、dC₀/dG₀がどうなるんだということですが、これについては、先ほど導出したC₀=(β(1+i)P₀/P₁)^σC₁をみていただきたいのですが、今の場合、価格が完全に硬直的なので、C₀は変わらないことがわかります。そのため、dC₀/dG₀=0となり、トータルとしても、

となります。要は価格が完全に硬直的な今回のような場合には、G₀の増加に対する労働需要と労働供給の増加のバランスするポイントは、買い手である家計の側にとっても、生産して財を供給する企業の側にとっても、丁度影響があった分を補うだけの結果を生むということになります。

さて、では実際の研究では、完全に価格が伸縮的なモデルや、ある程度の価格硬直性がある（徐々に価格が調整されるような）モデルが用いられるわけですが、次にそういった場合にどうなるのかをみていこうと思います。とりあえず、完全に価格が伸縮的になるλ=0の場合をみてみようと思います。

この場合も、影響を受けるのはフィリップス曲線になるのですが、一度最終的なフィリップス曲線の式の形の１つ前に戻って、

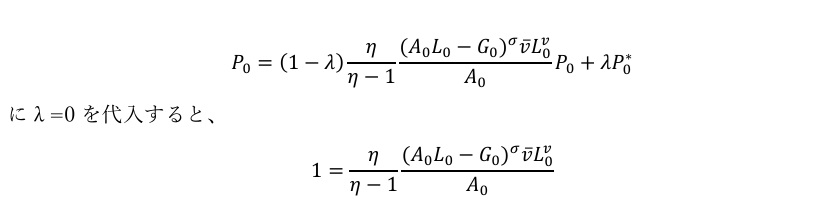
とかけます。これはつまり、縦に一直線なフィリップス曲線になるということになります。グラフにすると図表4のようになります。

　　　　　　　図表4. AS-ADダイアグラム（λ＝0のケース）

（出所）筆者作成

今回の場合も、G₀が増加すると労働需要・労働供給ともに増加します。ただ、今回の場合には、価格が伸縮的であるため、価格の調整も同時に行われ、今の場合は価格の上昇方向に調整されて、C₀にとっては下押し要因になります。価格が完全に硬直的な場合にはC₀は全く影響を受けないのですが、伸縮的な場合には労働需要・労働供給のバランスするポイントは、完全にはC₀の減少をカバーするにはいたらず、結果としてC₀は減少します。つまり、先ほどのdC₀/dG₀がマイナスという結果になります。

その中間（0＜λ＜1）の場合にも、結果は同じように、dC₀/dG₀はマイナスになります。因みに、ここまで書いてきたグラフとしては、図表5のようになります。

　　　　　　　図表5. AS-ADダイアグラム（0＜λ＜1のケース）

（出所）筆者作成

ここまでの結果を踏まえると、新古典派的なモデルやニューケインジアン型のモデルでは、dY₀/dG₀は1よりも小さいということになります。実際に初期の研究ではそういった結果が得られていて、例えばBaxter and King(1993)では、新古典派的なモデルを用いてシミュレーションを行い、政府消費、労働供給、生産の間には正の相関、つまり政府消費の増加は将来の増税をもたらし、恒常所得を減少させるために労働供給が増加して、それにより生産も増加することを示し、一方で家計の消費は減少することを示しています。また、Gali,Lopez-Salido, and Valles(2007)ではニューケインジアンモデルでによる分析を行い、標準的なニューケインジアンモデルの場合には、やはり政府消費の増加に対して、家計の消費が減少することを示しています（実は標準的なモデルを変更することで結果が変わるということがこの論文の主要な部分なのですが…それは今後扱います）。

では、実証分析ではどのような結果が得られているのでしょうか（言ってしまった気もしますが（笑））・・・というところですが、そこは次回に回そうと思います。

参考文献

Baxter, M., and R.G. King(1993).”Fiscal Policy in General Equilibrium,”American Economic Review, 83(3),315-334.

Galí, Jordi, J. David López-Salido, and Javier Vallés(2007).”Understanding the Effects of Government Spending on Consumption,” Journal of the European Economic Association,5(1),227–270.